I. Funciones matemáticas, computacionales, programáticas y paradigmáticas#

Cuando cotidianamente hablamos de la «función (de algo)», podemos decir que nos estamos refiriendo a la operación que se realiza sobre un objeto para obtener un resultado deseado. La función del refrigerador, por ejemplo, consiste en mantener una determinada temperatura en su interior, es decir, refrigerar. Como resultado, los alimentos que guardamos en él se conservan en buen estado. Siguiendo esta línea, podemos esquematizar la función del refrigerador («refrigeración») de la siguiente manera:

Alimento → Refrigeración → Conservación del alimento

Ilustrativamente, podemos también representar este esquema bajo la siguiente forma:

Donde de la generalización del esquema inicial, se desprende que la función denota la operación o serie de operaciones que se realizan sobre un valor de «entrada» (en nuestro ejemplo, los alimentos) para dar como resultado un valor de «salida» (la conservación del alimento a baja temperatura). En otras palabras, el núcleo de una función está en definir una o más operaciones que se realizan con el valor de entrada para transformarlo de alguna forma y dar como resultado un valor de salida. Pongamos varios ejemplos para asimilar esto de mejor manera:

Entrada («input») → Función («computación», «algoritmo») → Salida («output»)
Ingredientes → Receta (preparación) → Pizza
Libro → Lectura (interpretación) → Aprendizaje
Inversión → Producción → Negocio
Hipótesis → Experimentación → Descubrimiento científico
Ley (Poder Legislativo) → Interpretación (P. Judicial) → Ejecución (P. Ejecutivo)

A su vez, cualquiera de estas funciones puede descomponerse en muchas otras. Por ejemplo, podemos descomponer cada parte del paradigma estatal anterior según el funcionamiento interno de cada Poder:

Propuesta de ley → Revisión (votación, aprobación) → Nueva ley
Ley → Interpretación → Sentencia, jurisprudencia
Sentencia → Ejecución de la sentencia → Justicia

Como decía, esta forma paradigmática —modélica, base— de entender la función nos dará la clave para entender una infinidad de conceptos y fenómenos en un número de disciplinas. En realidad, la génesis de esta idea de función está en las matemáticas. Más particularmente, en un manuscrito de 1673 pergeñado por el gran Gottfried Leibniz, el cual se titula Methodus tangen­tium inversa seu de functionibus («el método inverso de tangentes, o sobre las funciones») [Herrera Castillo, 2013, Scriba, 1964].

Desarrollado ulteriormente por otro coloso —nuestro maestro Leonhard Euler—, este entendimiento de la función tiene precisamente el mismo sentido que le hemos estado dando. Para no perder el rigor, especifiquemos brevemente a qué nos referimos. Aunque haya diferentes formas de definir una función matemática, utilicemos la más común: la función es una relación unívoca de dependencia entre un elemento de un conjunto y otro elemento de otro conjunto.

Vayamos por partes: los conjuntos son grupos o colecciones de números, elementos u objetos con características en común. Los números pares, por ejemplo, pueden entenderse como un conjunto: $\{2,4,6,...\}$. La definición del conjunto «números pares» expresa claramente que dicho conjunto solo puede contener números que tienen como múltiplo al número dos.

Luego, se dice que hay una relación entre elementos de un conjunto con elementos de otro. Siguiendo nuestro ejemplo, puedo decir que el conjunto $\{6,12,18,...\}$ está relacionado con el conjunto de los números pares en función de una multiplicación por el número $3$. Así, el conjunto de los números pares sería la entrada, y este segundo conjunto sería la salida. En ese sentido, la relación entre los elementos de ambos conjuntos se da según las reglas u operaciones que una función define (en este caso, una multiplicación por $3$). Cada valor de salida depende enteramente de las operaciones que se realicen con el valor de entrada, y esta dependencia es unívoca porque a cada valor de entrada únicamente puede corresponderle un valor de salida. Es imposible, por ejemplo, que al número $2$ como valor de entrada, le correspondan los números $7$, $10$ y $24$ del conjunto de salida, puesto que $2\times 3=6$, de manera que exclusivamente el número $6$ del conjunto de salida le corresponde al $2$. En una palabra: la multiplicación es una función, y cuando multiplicamos solo podemos tener un único resultado válido como respuesta.

En matemáticas, veremos asimismo que la notación y representación de una función tienen una forma particular. La notación matemática más común para denotar una función es $f(x)$; su representación más común es una gráfica con coordenadas cartesianas. Ejemplifiquemos con el caso $f(x)=x^2$. Según nuestro esquema, la entrada es cualquier número (que representaremos con una $x$), la operación (función) que realizaremos sobre ella es elevarla al cuadrado, lo cual tendrá como resultado (salida) otro número, que podemos denominar con la letra $y$:

El hecho de que esta notación matemática pueda parecernos confusa se debe a su nivel de abstracción. En realidad, el uso de letras ($x,y$, etcétera) en lugar de números es una convención académica utilizada para facilitar la definición de reglas generales. Dichas letras comunican al lector que son variables, es decir, que su valor puede variar dependiendo del contexto. Las matemáticas siempre demandan la generalización de las formulaciones y expresiones propias de su campo, de manera que este tipo de «tecniquerías» son indispensables. Por lo demás, sería increíblemente trabajoso —e incluso confuso— escribir expresiones matemáticas complejas con un estilo diferente (e. g., «si tenemos una función matemática de cualquier número que es igual a dicho número elevado al cuadrado») al tradicional $f(x)=x^2$ (se lee: «efe de equis igual a equis cuadrada»).

A veces, la función se acompaña de la definición de su dominio, es decir, se puede señalar qué tipo de objeto es la entrada que introduciremos en la función. Por ejemplo:

Donde $\in$ significa «pertenece a» y $\mathbb{R}$ se utiliza para representar a los números reales. Entonces la última expresión la leeríamos como «donde equis pertenece al conjunto de los números reales».

Un principio elemental de la comunicación es la economía del lenguaje: el lenguaje siempre debe ser lo más claro y simple posible. Paradójicamente, esta notación es la más simple que existe, y cualquier otra forma de comunicar fórmulas matemáticas sería ineficiente y confusa. En realidad, la notación matemática solo nos resulta extraña por falta de hábito y eso es algo completamente normal.

Volviendo a lo nuestro, veamos por fin la representación gráfica de una función matemática:

!pip install matplotlib --upgrade

import math
import numpy as np
import pandas as pd
import seaborn as sns
import random
import torch
from torch import nn
import torchvision
from torchvision import transforms
import requests
from pathlib import Path
import matplotlib.pyplot as plt

# Para representar gráficamente la función, traduciremos ahora esto a código:

def f(x): # <- Definimos una función de x
  return x**2 # <- El resultado de esa función es x al cuadrado

# Ahora creamos nuestros valores usando la función:
xs = np.arange(0, 11, 1) #<- Las X serán números del 0 al 10 con intervalos de 1
ys = f(xs) # <- Las Y serán el resultado de aplicar la función a las X

# Graficamos las xs y las ys:
fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Valores de x')
ax.set_ylabel('Valores de y')
ax.hlines(y=16, xmin=0, xmax=4, linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=4, ymin=0, ymax=16, linewidth=1, color='white', linestyles='dashed')
plt.show()

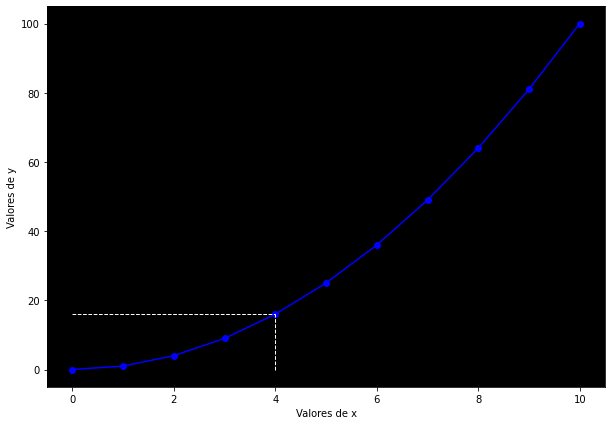
En la gráfica anterior, el eje horizontal representa los valores de $x$; el vertical, los de $y$. Lo que cada punto nos dice es que, por ejemplo, cuando $x$ vale 2, entonces $y$ vale 4; cuando $x$ vale 4, entonces $y$ vale 16; y así sucesivamente. Esto es así porque nuestra función indica que $y$ es el resultado de elevar $x$ al cuadrado. Finalmente, trazamos una línea azul que une todos los puntos para representar la tendencia que siguen; de igual forma, trazamos una línea blanca punteada para señalar al azar una intersección de las $x$ con las $y$.

# Podemos también representar esto como una tabla:

d = {'Valores de x': xs, 'Valores de y': ys}
tabla = pd.DataFrame(data=d)
tabla = tabla.style.hide_index()
tabla

Como se ve, nuestros valores de $y$ son el resultado de la función $f(x)=x^2$. La $x$ va tomando el valor de cada número que va del 0 al 10 y, como consecuencia, sobre él se realiza la operación que define la función para finalmente dar un resultado. Mostremos algunas equivalencias nuevamente:

La función es exactamente la misma tanto en la notación matemática, como en la notación programática, en la gráfica que hicimos, en la tablita de arriba y en este último esquema. Al final, solo estamos utilizando distintos signos propios de nuestros lenguajes (números, letras, líneas, flechas) para representar lo mismo de distintas maneras. Todas estas formas de representación son válidas, pero usaremos una u otra dependiendo del contexto y de nuestro propio gusto.

En este punto, merece la pena apuntar que «abstracto» es, por definición, una forma de representar simbólicamente ideas u objetos de la realidad. Etimológicamente, la palabra «abstraer» se compone de ab- —«alejar», «alejado (de algo)»— y trahēre —«arrastrar», «tirar (de algo)»—, de manera que «abstraer» significa arrastrar algo fuera de su forma primigenia. Abstraer, pues, implica separar algo de sus demás partes o de su situación inicial para representarlo de otra forma. En aritmética, por ejemplo, se separan las propiedades numéricas de las propiedades cromáticas, sensitivas, químicas, nutrimentales de dos pares de manzanas para representar —e incluso generalizar— de manera abstracta (i. e., mediante signos «$2,+,4$») las propiedades estrictamente matemáticas de esos dos pares, como $2+2=4$.

En algún momento, las propiedades numéricas de distintos objetos llegaron a consolidarse de tal forma que una nueva ciencia se constituyó, disociada de nuestro criterio personal y de las formas físicas concretas de nuestro entorno. Esa nueva ciencia, soberana sobre su propio campo, fue y sigue siendo hoy capaz de ir descubriendo nuevas configuraciones matemáticas a través de las relaciones y operaciones que pueden darse dentro de sí misma, sin atención explícita a la realidad que la rodea; pero este proceso «artificioso» o formal no debe llevarnos nunca a creer que las operaciones matemáticas tienen que ver con realidades distintas a la nuestra. Todo pensamiento posible, sea científico, delirante o fantasioso, toma siempre origen a flor de tierra, por mucho que nuestros aparatosos sistemas de pensamiento aparenten lo contrario.

Para abundar en el tema de las formas de representación, léase Poetizar de Gustavo Bueno.

Graficación de funciones

Finalmente, me gustaría utilizar este nuevo aprendizaje para fortalecer nuestra intuición sobre la graficación de las funciones. O sea, veremos por qué la función cuadrática es una parábola, por qué la sigmoide parece una letra S, etcétera. Esto tiene que ver con el comportamiento de la función: la gráfica representa el patrón que —gracias a la función— resulta de las intersecciones entre los valores de $x$ y los valores de $y$.

# Ya vimos una parte de la función cuadrática, pero ahora veámosla con más valores
def f(x):
  return x**2

xs = np.arange(-20, 21, 1) # Nuestras X ahora irán del -20 al 20 en intervalos de 1
ys = f(xs)

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Valores de x')
ax.set_ylabel('Valores de y')
ax.hlines(y=ys[5], xmin=0, xmax=xs[5], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=xs[5], ymin=0, ymax=ys[5], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=0, ymin=0, ymax=400, linewidth=1, color='white', linestyles='dotted')
ax.hlines(y=0, xmin=xs[0], xmax=xs[-1], linewidth=1, color='white', linestyles='dotted')
plt.show()

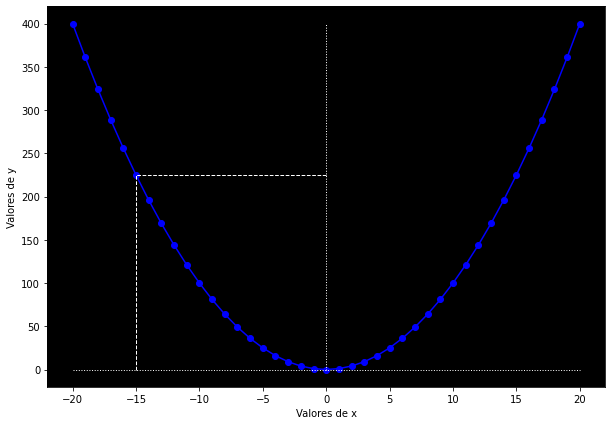
Una función cúbica:

def cubica(x):
  return x**3

ys = cubica(xs)

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Valores de x')
ax.set_ylabel('Valores de y')
ax.hlines(y=ys[5], xmin=0, xmax=xs[5], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=xs[5], ymin=0, ymax=ys[5], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=0, ymin=ys[0], ymax=ys[-1], linewidth=1, color='white', linestyles='dotted')
ax.hlines(y=0, xmin=xs[0], xmax=xs[-1], linewidth=1, color='white', linestyles='dotted')
plt.show()

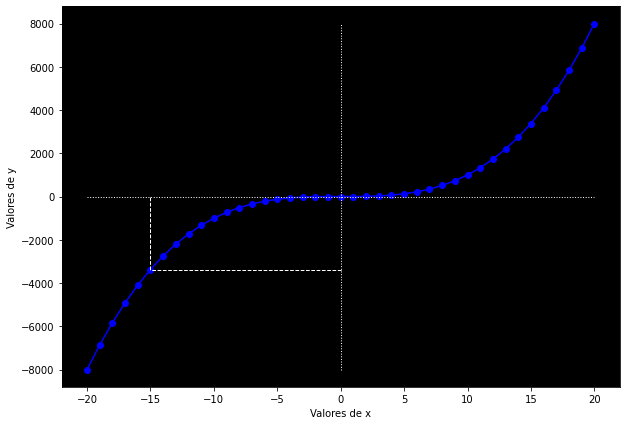
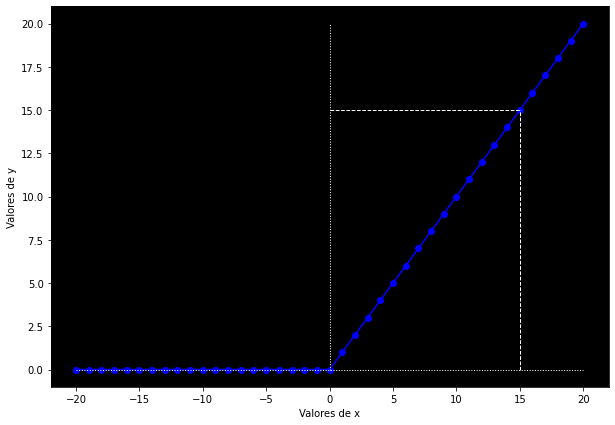
La función de activación ReLU (Rectified Linear Unit, «unidad lineal rectificada»), ampliamente utilizada en deep learning, se define como:

Su función es convertir en 0 todos los números negativos y reservar su valor original a los positivos. En la fórmula podemos apreciar que por cada número que entra en la función, el resultado es el valor máximo entre $0$ y el valor de entrada: si el valor de entrada es $-1$, entonces el resultado es $0$ (porque $0$ es mayor que $-1$); de igual forma, si el valor de entrada es $1$, entonces el resultado será $1$ (porque $1>0$).

def ReLU(x):
  return np.maximum(0, x)

ys = ReLU(xs)

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Valores de x')
ax.set_ylabel('Valores de y')
ax.hlines(y=ys[-6], xmin=0, xmax=xs[-6], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=xs[-6], ymin=0, ymax=ys[-6], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=0, ymin=ys[0], ymax=ys[-1], linewidth=1, color='white', linestyles='dotted')
ax.hlines(y=0, xmin=xs[0], xmax=xs[-1], linewidth=1, color='white', linestyles='dotted')
plt.show()

Incluso podemos graficar funciones que matemáticamente podrían parecernos jeroglíficos, pero que programáticamente son bastante sencillas. La función softmax está dada por:

Para entenderla mejor, podemos hacer un desglose de sus términos:

En términos simples, esta fórmula dice que la función softmax consiste en dividir el número $e$ elevado a la potencia $x_i$ –es decir, a la potencia del valor correspondiente de $x$— entre la sumatoria de todos los valores de $x$ como potencias del número $e$. Si lo escribiéramos paso por paso, quedaría como:

Supongamos que nuestras $x$ son los números del -2 al 1, entonces reemplazamos valores y aplicamos la fórmula:

Nuestros resultados —o valores de $y$, si se quiere— serían 0.032, 0.087, 0.236 y 0.643, respectivamente. Los valores sumados entre sí siempre dan 1 cuando les aplicamos la función sotfmax.

Ahora podemos apreciar mejor la simplicidad de la fórmula inicial, en comparación al trabajoso desglose que debemos hacer al momento de calcular valor por valor. Esta es una de las razones por las que la notación matemática es tan abstracta.

Afortunadamente, Python nos evita todo este desparpajo. Podemos delegar a nuestro programita el cálculo de esta fórmula enredosa y desgastante:

def Softmax(x):
  return np.exp(x) / sum(np.exp(x))

ys = Softmax(xs)

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Valores de x')
ax.set_ylabel('Valores de y')
ax.hlines(y=ys[-3], xmin=0, xmax=xs[-3], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=xs[-3], ymin=0, ymax=ys[-3], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=0, ymin=ys[0], ymax=ys[-1], linewidth=1, color='white', linestyles='dotted')
ax.hlines(y=0, xmin=xs[0], xmax=xs[-1], linewidth=1, color='white', linestyles='dotted')
print(f'Todos los valores de y sumados siempre dan como resultado: {np.sum(ys)}.\n')

Todos los valores de y sumados siempre dan como resultado: 1.0.

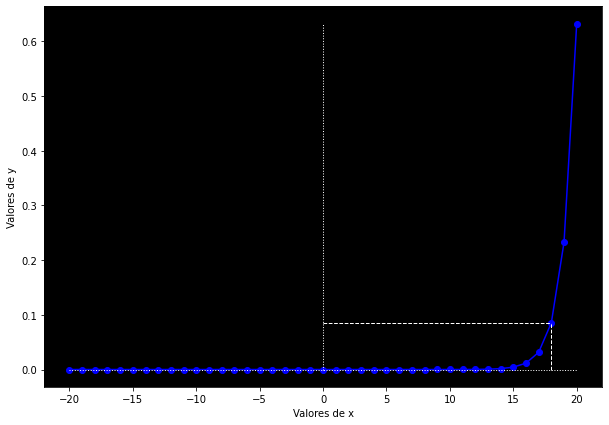
En primer lugar, enfoquémonos en entender que estas funciones implican un patrón, el cual define la manera en que obtendremos $y$.

Ahora, ¿de dónde sale todo esto y qué quiere decir? La respuesta depende también de lo que queramos hacer con nuestro aprendizaje. Primero, subrayemos nuevamente que todos estos signos son maneras de representar. Descubrir algo o hablar de algo novedoso, implica también la necesidad de buscar una forma de comunicar esa novedad. Naturalmente, comunicar esa novedad conlleva formular nuevos conceptos, ideas y expresiones para poder comunicarla; de otra forma, sería imposible diferenciarla de lo que ya conocemos.

En ese sentido, los primeros matemáticos que trataron de entender el concepto de función buscaron también una forma de expresarlo. Acaso por azar, por facilidad, por la autoridad del grandioso Leonhard Euler o por cientos de posibles razones más, la notación que finalmente convinieron todos en utilizar fue $f(x)$. De igual manera, las formas geométricas, textuales o programáticas de representarla también son una convención, así como estas letras, tildes y comas que escribo también lo son. Está siempre fuera de nosotros la «decisión» objetiva sobre qué convenciones permanecen y qué otras desaparecen. De cualquier manera, cada persona entiende y representa de diferente forma todas estas cosas para sus adentros.

Por otro lado, como digo, su uso dependerá de nosotros. En el caso de una función, por ejemplo, a un matemático le interesan las propiedades lógicas, numéricas, geométricas y abstractas de la función; a un informático, saber qué es una función y cómo se relaciona eso con el funcionamiento de una computadora; a un programador, saber qué propiedades tienen las funciones de cierto lenguaje. Nosotros podemos darles esa o cualquier otra utilidad que nos venga en gana.

Digamos, por ejemplo, que acabamos de descubrir que los lenguajes cambian a un ritmo que se puede representar con una función sigmoide: primero, nadie utiliza la expresión que queremos estudiar; en algún momento, una nueva expresión aparece y comienza a utilizarse por unas cuantas personas; después, llega un punto en el que se extiende rápidamente entre la población; y finalmente, al adoptarse universalmente, su uso cambia muy poco, puesto que ya nadie deja de usarla, ni tampoco nadie comienza a usarla por primera vez.

La fórmula para generar una gráfica de esta naturaleza es:

Programáticamente:

def Sigmoide(x):
  return 1 / (1 + np.exp(-x))

ys = Sigmoide(xs)

fig, ax = plt.subplots(figsize=(10, 7))
ax.plot(xs, ys, marker='o', color='blue') 
ax.set_facecolor('black')
ax.set_xlabel('Línea del tiempo')
ax.set_ylabel('Número de personas que utilizan la nueva palabra')
ax.hlines(y=ys[20], xmin=0, xmax=xs[20], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=xs[20], ymin=0, ymax=ys[20], linewidth=1, color='white', linestyles='dashed')
ax.vlines(x=0, ymin=ys[0], ymax=ys[-1], linewidth=1, color='white', linestyles='dotted')
ax.hlines(y=0, xmin=xs[0], xmax=xs[-1], linewidth=1, color='white', linestyles='dotted')
plt.show()

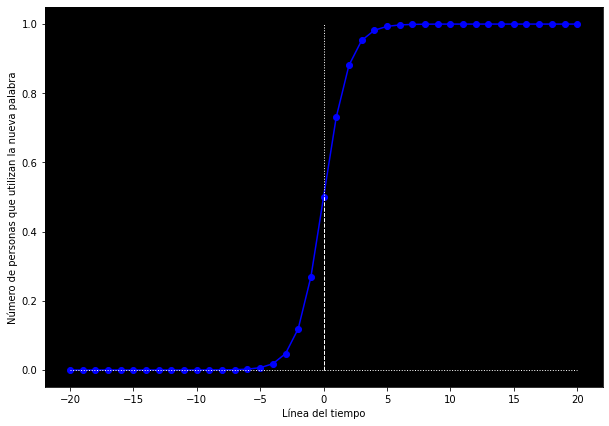
Como decíamos: primero nadie la usa, después pocas personas, luego crece rápidamente y al final se estanca. En este caso, $x$ representa el paso en el tiempo e $y$ el número de personas que utilizan una palabra.

Esta función puede utilizarse para representar el número de infectados por COVID-19, el desarrollo de un embrión, el crecimiento de una nueva industria y miles cosas más. De la misma manera, se le pueden dar usos más complejos: por ejemplo, se puede utilizar para diagnosticar enfermedades con modelos matemáticos (modelos de inteligencia artificial). Su utilidad depende enteramente de nosotros.

II. Algoritmos#

Para hablar de algoritmos nos atendremos a lo que Donald Knuth —prominente programador— ha sentenciado sobre ellos. En esencia, un algoritmo consiste en un conjunto finito de reglas o instrucciones ordenadas cuyo fin es resolver un tipo de problema específico.

Según Knuth, todo algoritmo debe ofrecer una solución concreta al problema que se proponga resolver; además, debe ser definido, es decir, preciso, no ambiguo; también ha de ser efectivo, en el sentido de que las operaciones que contiene sean lo suficientemente básicas para que puedan realizarse en un periodo finito de tiempo por cualquier persona; finalmente, debe contener una «entrada» y una «salida», términos con los que ya estamos familiarizados.

Para ilustrar este concepto, podemos comenzar con un ejemplo simple de algoritmo. Digamos que nos interesa crear un algoritmo para colocarnos un zapato. Podríamos esbozar el siguiente esquema:

1. Tomar el zapato con ambas manos.
2. Apuntar el talón del zapato hacia nosotros.
3. Meter la punta de nuestro pie dentro del zapato.
4. Cambiar el agarre para sostener el zapato con los pulgares dentro de él.
5. Meter nuestro pie hasta el fondo del zapato al tiempo que sacamos los pulgares.

Como vemos, la naturaleza del algoritmo es bastante simple, aunque su formulación no es nada sencilla. En rigor, un algoritmo solo funciona cuando verdaderamente satisfacemos los requisitos que mencionábamos antes. El algoritmo para colocar zapatos que acabamos de sugerir podría fallar de mil maneras: ¿cómo distingo el zapato izquierdo del derecho? ¿Cómo elijo cuál par de zapatos usar? ¿Qué pasa si se me cae el zapato de las manos durante el paso 2? Aunque humanamente podamos improvisar o razonar cada paso, una computadora no puede hacerlo, de manera que nuestro algoritmo quedaría inutilizado ante cualquier imprevisto.

Podríamos decir también que, a pesar de ciertas diferencias sutiles, un algoritmo y una función son lo mismo: una operación realizada con una entrada para dar resultado a una salida.

Dicho esto, me parece que este esbozo es suficiente por el momento para entender al algoritmo. Aunque el algoritmo sea una especie de receta o instructivo sencillo para resolver un problema concreto, su complejidad radica en el nivel de detalle minucioso que requiere para ser efectivo. A mi entender, el algoritmo es el uso mecánico de la fuerza bruta para conseguir un fin; pero esa fuerza bruta debe estar calibrada meticulosamente.

Finalmente, ejemplifiquemos con un algoritmo verdadero. Formularemos el famoso algoritmo de Euclides, utilizado para encontrar el máximo común divisor de dos números.

Aunque la notación algorítmica nos pueda resultar más familiar, es necesario advertir que el signo «←» puede llegar a ser confuso porque indica una secuencia de derecha a izquierda. Este signo indica que el valor de la izquierda adquiere el valor de la derecha: «n ← r» significa «n adquiere el valor de r»; el signo «↔», por otra parte, significa que debemos intercambiar el valor de las variables entre sí.

Ahora sí, el algoritmo: Dados dos números positivos enteros $m$ y $n$, el Algoritmo E —de Euclides— encontrará el máximo común divisor entre ellos, es decir, encontrará el entero positivo más grande que puede dividir a ambos sin ningún residuo.

Algoritmo E:

E0. Comprobar que $m\ge n$. Si $m<n$, intercambiar $m\leftrightarrow n$.

E1. Encontrar el residuo. Dividir $m$ entre $n$; el residuo será $r$. (Tendremos que $0\le r<n$).

E2. ¿Es cero? Si $r=0$, el algoritmo termina; $n$ es la respuesta.

E3. Reducir. Ahora $m\leftarrow n,n\leftarrow r$, y volveremos al paso E1.

En pseudocódigo:

Función AlgoritmoE(m, n):

Si m es menor que n:
  intercambiar valores 
  r = m módulo n
  si r es igual a 0:
    el resultado es n
  en caso contrario:
    mientras r no sea igual a cero:
      intercambiar los valores de m, n por los de n, r
      r = m módulo n
      si r es igual a 0:
        el resultado es n

El algoritmo impone condiciones, reglas y se anticipa a determinadas situaciones para funcionar. Aunque el «ambiente matemático» sea muchísimo más predecible que el «vital» (es decir, en el algoritmo pasado se nos podía caer el zapato, pero en este algoritmo no se desaparecerá ningún número), lo cierto es que incluso formular algoritmos de esta naturaleza es un arte menor que requiere de cierta práctica.

En Python, podríamos programarlo de la siguiente forma:

def AlgoritmoE(m, n):
  if m < n:
    m, n = n, m
  r = m%n
  if r == 0:
    return n
  else:
    while r != 0:
      m, n = n, r
      r = m%n
      if r == 0:
        return n

# Una versión simplificada del algoritmo:

def Euclides(a, b):
    while b != 0:
        a, b = b, a % b
    return a

# Ponemos a prueba los algoritmos:

resultados_1 = AlgoritmoE(544, 119), AlgoritmoE(2166, 6099)
resultados_2 = Euclides(544, 119), Euclides(2166, 6099)

print(f'Resultados del primer algoritmo: {resultados_1} | Resultados del segundo algoritmo: {resultados_2}')

Resultados del primer algoritmo: (17, 57) | Resultados del segundo algoritmo: (17, 57)

A mi juicio, el algoritmo más importante de la historia es la máquina de Turing. Este algoritmo definió un modelo para las computadoras de nuestros días, y su simplicidad es igual de impresionante que su capacidad.

Para saber en qué consiste ese algoritmo, léase: The Annotated Turing de Petzold.

III. Programación#

Entre otras cosas, para nosotros el interés del algoritmo o de la función radica precisamente en que nos permiten entender el potencial de la máquina más avanzada de nuestros días. La programación, por su parte, nos permite materializar o aprovechar ese entendimiento.

En esencia, programar implica comunicar instrucciones (algoritmos, funciones) a una computadora. Las instrucciones formuladas en un lenguaje de programación se traducen mediante un compilador (es decir, otro programa) al «lenguaje máquina», es decir, a un sistema binario que luego puede ser «interpretado» por los transistores del microprocesador.

Como es sabido, el sistema binario que utilizan las computadoras consiste de ceros y unos. Por ejemplo, los números del 0 al 8 serían:

0. 0 0 0
1. 0 0 1
2. 0 1 0
3. 0 1 1
4. 1 0 0
5. 1 0 1
6. 1 1 0
7. 1 1 1
8. 1 0 0 0

Tomemos el siguiente número del sistema decimal:

Aquí, el 3 está en el lugar de las unidades; el dos, en las decenas; y el tres, en las centenas. Entonces,

Cada lugar de cada dígito representa una potencia de 10, por lo que hay diez posibles dígitos en cada lugar (ahora ya empieza a tener sentido el término «sistema decimal»). El primer lugar de la derecha representa un ${10}^0$; el de en medio, ${10}^1$; el tercero, ${10}^2$, y así sucesivamente:

En binario, por otro lado, solo tenemos dos dígitos y los exponentes del dos en cada lugar:

Que es equivalente a:

Entonces, si quisiéramos representar el valor decimal 3, tendríamos que añadir 2 y 1 en sistema binario así:

Y el valor decimal 123:

La mayoría de las computadoras utilizan 8 dígitos o bits (lo cual quiere decir «dígito binario», en inglés «binary digit») a la vez, de manera que el número 3 sería 00000011. Cada conjunto de 8 bits se denomina byte.

Aunque en los humanos el sistema decimal prevalezca por sernos más intuitivo, lo cierto es que una vez más estamos hablando de una convención. Xul Solar, por ejemplo, fue un hombre singular que sostuvo durante mucho tiempo que el sistema duodecimal de numeración es superior al decimal. En su vida personal y profesional, Xul Solar utilizaba ese sistema.

El sistema binario, por otro lado, es especialmente conveniente para las computadoras por la sencilla razón de que facilita la traducción de ceros y unos a señales eléctricas: el cero indica apagado; el uno, encendido. El transistor cumple con la función de representar eléctricamente los unos y ceros de la computadora, realizando operaciones con ellos al prenderse y apagarse continuamente. Un procesador de computadora está compuesto de millones de transistores representando unos y ceros. Un transistor puede representar cientos de miles de millones de ceros y unos por segundo; el transistor más pequeño de nuestros días es más o menos 50,000 veces más delgado que un cabello.

El sistema binario fue formulado nada más y nada menos que por nuestro viejo amigo Leibniz, quien también probablemente utilizó el término «algoritmo» en sentido moderno por primera vez. Leibniz fue colega de Johann Bernoulli, quien a su vez fue mentor de nuestro otro amigo Leonhard Euler.

Naturalmente, el sistema binario, además de representar números, puede también representar letras, imágenes, videos, música y todo aquello que vemos en la pantalla de una computadora. Para ello, se han convenido distintas combinaciones de código binario para representar ciertos caracteres. La letra «A», por ejemplo, se representa con el número 65, que en binario es 01000001; ASCII y Unicode son códigos estándar para representar el alfabeto y algunos caracteres especiales.

Por otro lado, el estándar para representar colores es RGB, el cual indica la cantidad de rojo, verde y azul que contiene el color a representar. Cada píxel de las pantallas de las computadoras utiliza tres bytes para representar un color. Veamos esto ejemplificado con la imagen de un número:

from torchvision import datasets
from torchvision.transforms import ToTensor

test_data = datasets.MNIST(
    root = 'data',
    train = False,
    transform = ToTensor(),
    download = True,
    target_transform = None)

from torch.utils.data import DataLoader
 
BATCH_SIZE = 32

test_dataloader = DataLoader(dataset=test_data,
                             batch_size=BATCH_SIZE,
                             shuffle=False)

test_features_batch, test_labels_batch = next(iter(test_dataloader))
image = test_features_batch[4]
plt.imshow(image.squeeze().cpu(), cmap='gray')

<matplotlib.image.AxesImage at 0x7f759b285650>

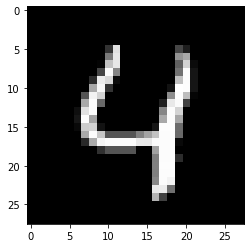
Ahora veamos más de cerca el valor de cada píxel si consideramos una escala de colores del 0 (blanco) al 1 (negro):

df.style.set_properties(**{'font-size':'6pt'}).background_gradient('Greys')

Mientras más nos acercamos a la imagen, mejor vemos los píxeles (los pequeños cuadros coloreados) que representan el número. Así, sabemos ya que la máquina más poderosa creada por el humano consiste en enormes secuencias de números.

El problema radica precisamente en eso: estas secuencias son gigantescas, de manera que comunicarnos con la computadora en ese lenguaje sería un martirio. Por ello, los lenguajes de programación facilitan dicha comunicación, puesto que la computadora sabe traducir a su lenguaje las instrucciones que le damos mediante un programa. Como veremos más adelante, apenas unas cuantas líneas de código son necesarias para crear un programa de inteligencia artificial.